Mehr Informationen finden Sie im Portal Lernen sichtbar machen
Interpretationshilfe zum Robustheitsindex: Unterschied zwischen den Versionen
Beywol (Diskussion | Beiträge) (Leere Seite erstellt) |
Beywol (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| + | ====Was ist eine Effektstärke (z.B. ''d'' )?==== | ||
| + | Die Effektstärke zeigt in ''Lernen sichtbar machen'' in der Regel an, wie gross der Unterschied ist, den ein Faktor (meist eine unabhängige, ursächlich wirkende Variable) auf die Verteilung einer anderen Variablen (meist eine abhängige) auslöst (z. B. Einfluss des Faktors „Feedback der Lehrperson“ auf Lernleistungen der Schülerinnen und Schüler). | ||
| + | <br>Gekennzeichnet wird dieser Wert u. a. mit ''d'' (je nach verwendeter Formel; Hattie verwendet die Formel von Cohen). | ||
| + | <br><br> | ||
| + | Video: [http://www.lernensichtbarmachen.ch/wp-content/uploads/2015/02/Effektstaerken_Hattie.ogv Was ist eine Effektstärke?] | ||
| + | <br><br> | ||
| + | ''siehe auch'' [[Effektstärke]], [[Berechnung der Effektstärken in der Hattie-Studie - Lesebeispiel Teil I]], [[Berechnung der Effektstärken in der Hattie-Studie - Lesebeispiel Teil II]] | ||
| + | <br><br> | ||
| + | Zur Veranschaulichung der Effekte nutzt Hattie ein Barometer (siehe Abbildung; Hattie 2013, S. 24), welches er in verschiedene Bereiche unterteilt. Diese Bereiche werden nachfolgend, angelehnt an Hatties Ausführungen, kurz erklärt. | ||
| + | <br> | ||
| + | |||
| + | [[Datei:Hattie_Barometer.jpg]] | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ====Erwünschte Effekte (''d'' > 0,40)==== | ||
| + | Einflüsse oberhalb ''d'' = 0,40 haben die grössten Auswirkungen auf Lerneleistungs-Outcomes der Schülerinnen und Schüler. Hier wird die Lernleistung derart verbessert, dass wir in der realen Welt Unterschiede beobachten können. | ||
| + | <br><br> | ||
| + | |||
| + | ====Schulbesuchseffekte (''d'' = 0,15 bis ''d'' = 0,40)==== | ||
| + | Typische Effekte durch einen Schulbesuch bewegen sich zwischen ''d'' = 0,15 und ''d'' = 0,40. Jeder Einfluss innerhalb dieser Zone ist vergleichbar mit dem, was eine Lehrperson in einem typischen Schuljahr erzielen kann. | ||
| + | <br><br> | ||
| + | |||
| + | ====Entwicklungseffekte (''d'' = 0,00 bis ''d'' = 0,15)==== | ||
| + | Die Zone zwischen ''d'' = 0,0 und ''d'' = 0,15 entspricht dem, was Lernende vermutlich erreichen könnten, wenn kein Schulbesuch stattfinden würde. Allein schon aufgrund von Reifungsprozessen lässt sich ein Grossteil der Lernverbesserungen zurückführen. Daher können alle Effekte unterhalb von ''d'' = 0,15 als potenziell schädlich angesehen werden und sollten nicht umgesetzt werden. | ||
| + | <br><br> | ||
| + | |||
| + | ====Umkehrende Effekte (''d'' < 0,00)==== | ||
| + | Umfasst Effekte welche die Lernleistung verringern. Diese sind in jedem Fall unerwünscht. | ||
| + | |||
| + | <br><br> | ||
| + | |||
| + | ===Robustheitsindex=== | ||
| + | Kennzahl zu jedem der von John Hattie ausgewiesenen Einflussfaktoren (2023 neu eingeführt). Auf einer ganzzahligen Skala von 1 (sehr volatil/veränderlich) bis 5 (sehr robust/dauerhaft) ist ablesbar, wie stabil die ausgewiesene Effektstärke über die kommenden Jahre bzw. bei neu hinzukommenden Forschungen zu diesem Einfluss auf Lernleistungen voraussichtlich bleiben wird. <br> | ||
| + | Der Robustheitsindex ist ein gewichteter Durchschnitt von fünf Hauptindikatoren für Stabilität: | ||
| + | * Anzahl der vorliegenden Meta-Analysen, | ||
| + | * Anzahl der darin verarbeiteten Studien, | ||
| + | *(geschätzte) Gesamtzahl der Schülerinnen und Schüler, die in diese Studien einbezogen sind | ||
| + | * Anzahl der ausgewiesenen Effekte für diesen Einfluss | ||
| + | * die nach Verfahren von Rosenthal (1979) und Orwin (1983) geschätzte Anzahl minimal künftig neu hinzukommenden Studien, die zu einer deutlichen Veränderung der Effektstärke führen würde (je weniger, desto veränderlicher). = fehlschlussvermeidenden Anzahl von unveröffentlichten Studien / fail-safe studies. | ||
| + | Die Robustheitsindizes von 3, 4 und 5 sind aufsteigend zuverlässiger, hingegen schwanken solche mit Werten von 1 oder 2 eventuelle, wenn im Laufe der Zeit mehr Studien zu diesem Faktor dazu kommen. | ||
| + | Für den Faktor «Reziprokes Lehren» ist der Durchschnitt über die Quintile der fünf Indikatoren R=5, was auf eine hohe Robustheit hinweist. | ||
| + | |||
| + | <br><br> | ||
| + | |||
| + | ==Quellen== | ||
| + | *Hattie, John A. C. (2023): Visible Learning: The Sequel. A Synthesis of Over 2,100 Meta-Analyses Relating to Achievement. New York: Routledge. | ||
| + | *Orwin, Robert G. (1983). A fail-safe N for effect size in meta-analysis. Journal of Educational Statistics, 8(2), 157-159. | ||
| + | *Rosenthal, Robert (1979). The ‘file drawer problem’ and tolerance for null results. Psychological Bulletin, 86, 638–641. | ||
| + | |||
| + | |||
| + | <br><br> | ||
| + | __NOTOC__ | ||
Version vom 9. Juni 2023, 11:03 Uhr
Was ist eine Effektstärke (z.B. d )?
Die Effektstärke zeigt in Lernen sichtbar machen in der Regel an, wie gross der Unterschied ist, den ein Faktor (meist eine unabhängige, ursächlich wirkende Variable) auf die Verteilung einer anderen Variablen (meist eine abhängige) auslöst (z. B. Einfluss des Faktors „Feedback der Lehrperson“ auf Lernleistungen der Schülerinnen und Schüler).
Gekennzeichnet wird dieser Wert u. a. mit d (je nach verwendeter Formel; Hattie verwendet die Formel von Cohen).
Video: Was ist eine Effektstärke?
siehe auch Effektstärke, Berechnung der Effektstärken in der Hattie-Studie - Lesebeispiel Teil I, Berechnung der Effektstärken in der Hattie-Studie - Lesebeispiel Teil II
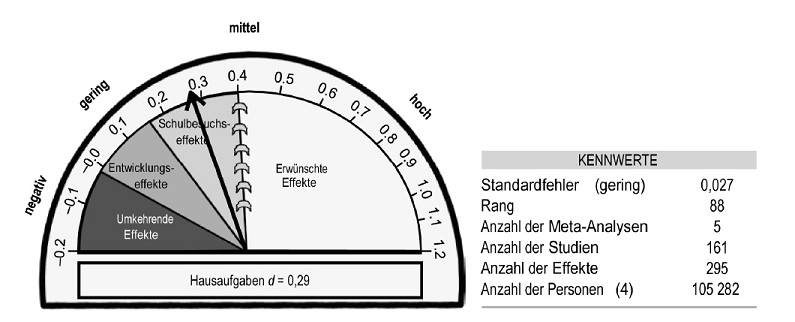
Zur Veranschaulichung der Effekte nutzt Hattie ein Barometer (siehe Abbildung; Hattie 2013, S. 24), welches er in verschiedene Bereiche unterteilt. Diese Bereiche werden nachfolgend, angelehnt an Hatties Ausführungen, kurz erklärt.
Erwünschte Effekte (d > 0,40)
Einflüsse oberhalb d = 0,40 haben die grössten Auswirkungen auf Lerneleistungs-Outcomes der Schülerinnen und Schüler. Hier wird die Lernleistung derart verbessert, dass wir in der realen Welt Unterschiede beobachten können.
Schulbesuchseffekte (d = 0,15 bis d = 0,40)
Typische Effekte durch einen Schulbesuch bewegen sich zwischen d = 0,15 und d = 0,40. Jeder Einfluss innerhalb dieser Zone ist vergleichbar mit dem, was eine Lehrperson in einem typischen Schuljahr erzielen kann.
Entwicklungseffekte (d = 0,00 bis d = 0,15)
Die Zone zwischen d = 0,0 und d = 0,15 entspricht dem, was Lernende vermutlich erreichen könnten, wenn kein Schulbesuch stattfinden würde. Allein schon aufgrund von Reifungsprozessen lässt sich ein Grossteil der Lernverbesserungen zurückführen. Daher können alle Effekte unterhalb von d = 0,15 als potenziell schädlich angesehen werden und sollten nicht umgesetzt werden.
Umkehrende Effekte (d < 0,00)
Umfasst Effekte welche die Lernleistung verringern. Diese sind in jedem Fall unerwünscht.
Robustheitsindex
Kennzahl zu jedem der von John Hattie ausgewiesenen Einflussfaktoren (2023 neu eingeführt). Auf einer ganzzahligen Skala von 1 (sehr volatil/veränderlich) bis 5 (sehr robust/dauerhaft) ist ablesbar, wie stabil die ausgewiesene Effektstärke über die kommenden Jahre bzw. bei neu hinzukommenden Forschungen zu diesem Einfluss auf Lernleistungen voraussichtlich bleiben wird.
Der Robustheitsindex ist ein gewichteter Durchschnitt von fünf Hauptindikatoren für Stabilität:
- Anzahl der vorliegenden Meta-Analysen,
- Anzahl der darin verarbeiteten Studien,
- (geschätzte) Gesamtzahl der Schülerinnen und Schüler, die in diese Studien einbezogen sind
- Anzahl der ausgewiesenen Effekte für diesen Einfluss
- die nach Verfahren von Rosenthal (1979) und Orwin (1983) geschätzte Anzahl minimal künftig neu hinzukommenden Studien, die zu einer deutlichen Veränderung der Effektstärke führen würde (je weniger, desto veränderlicher). = fehlschlussvermeidenden Anzahl von unveröffentlichten Studien / fail-safe studies.
Die Robustheitsindizes von 3, 4 und 5 sind aufsteigend zuverlässiger, hingegen schwanken solche mit Werten von 1 oder 2 eventuelle, wenn im Laufe der Zeit mehr Studien zu diesem Faktor dazu kommen. Für den Faktor «Reziprokes Lehren» ist der Durchschnitt über die Quintile der fünf Indikatoren R=5, was auf eine hohe Robustheit hinweist.
Quellen
- Hattie, John A. C. (2023): Visible Learning: The Sequel. A Synthesis of Over 2,100 Meta-Analyses Relating to Achievement. New York: Routledge.
- Orwin, Robert G. (1983). A fail-safe N for effect size in meta-analysis. Journal of Educational Statistics, 8(2), 157-159.
- Rosenthal, Robert (1979). The ‘file drawer problem’ and tolerance for null results. Psychological Bulletin, 86, 638–641.