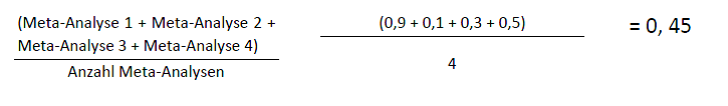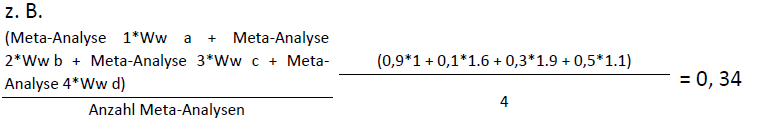Berechnung der Effektstärken in der Hattie-Studie - Lesebeispiel Teil I

Wie wird eine Effektstärke d in der Hattie-Studie errechnet? Was gilt es, bei der Interpretation einer so berechneten Effektstärke d zu beachten? Um diese Fragen zu beantworten, haben wir ein fiktives Lesebeispiel aufbereitet.


Die über die vier Meta-Analysen gemittelte Effektstärke (d) beträgt in diesem Beispiel d = 0,45 (rote Linie). Sie ist positiv, was bedeutet, dass sie einen positiven Einfluss auf die Lernleistungen von Lernenden hat. Förderlich fürs Lernen sind Einflussfaktoren (Faktor) mit positiven Effektstärken. Hatties Referenzwert für besonders beachtenswerte Faktoren sind solche mit einer Effektstärke über dem Umschlagpunkt (U-Punkt) von d = 0,4, was dem durchschnittlichen Lernzuwachs pro Schuljahr entspricht, wie er z. B. durch Instrumente wie die der internationalen Schulleistungsstudien wie PISA gemessen wird (Interpretationshilfe zur Effektstärke).

Schaut man sich in dem fiktiven Beispiel die untersuchten Meta-Analysen genauer an, ergibt sich ein differenzierteres Bild aus unterschiedlichen Werten. Jede der Säulen in Abbildung 1 steht für eine Meta-Analyse, die in die Berechnung der von Hattie für den Faktor ausgewiesenen Durchschnitts-Effektstärke eingeflossen ist. In unserem Beispiel sind es vier Meta-Analysen, aus denen die mittlere Effektstärke von d = 0,45 errechnet wird. Dabei weist die Meta-Analyse 1 eine dreimal höhere Effektstärke aus (d = 0,9), als die Meta-Analyse 3 (d = 0,3). Im Vergleich zur Meta-Analyse 2 (d = 0,1) ist die Effektstärke der Meta-Analyse 1 sogar neunmal so gross. Berechnet wird die gemittelte Effektstärke bei Hattie über den Mittelwert (Durchschnitt):

Aus dem Durchschnitt dieser vier Effektstärken resultiert die positive gemittelte Effektstärke von d = 0,45. In diesem Fall würde es sich lohnen, die einzelnen Meta-Analysen genauer zu untersuchen, um festzustellen, was die grossen Unterschiede in den einzelnen Effektstärken hervorbringt. So hätte man weitere Informationen für die Interpretation der gemittelten Effektstärke. Des Weiteren gilt es zu beachten, dass die Effektstärken der einzelnen Meta-Analysen ebenfalls einen Durchschnittswert aus deren Primärstudien darstellen (dazu im Lesebeispiel Teil II - Meta-Analysen in der Hattie-Studie mehr). Mittlere Effektstärken sind sinnvoll, um grosse Datenmengen zusammenzufassen und untereinander zu vergleichen. Um daraus Schlüsse für eine spezifische Situation zu ziehen (z. B. ob Hausaufgaben in der eigenen Klasse sinnvoll sind), bedarf es einer genaueren Betrachtung, die über Primärstudien führt, die Situationen möglichst ähnlich der eigenen Klasse untersuchen.

Eine Alternative zu der einfachen Mittelwertsbildung wie im Lesebeispiel wäre, die Meta-Analysen zu gewichten. Z. B. d-Werte aus Meta-Analysen durch Multiplikation mit einem positiven Wichtungswert (Ww) stärker in die gemittelte Effektstärke einfliessen zu lassen.

Der Wichtungswert würde z. B. steigen für Meta-Analysen,
1. die neueren Datums sind
2. viele Primärstudien enthalten
3. die Primärstudien mit vielen Teilnehmenden enthalten
4. die zuverlässigere Messinstrumente enthalten
5. deren Untersuchungsdesigns besser kontrolliert sind
6. usw.
Dieses Vorgehen wäre jedoch sehr aufwändig, müsste vielfach mit fehlenden Daten zurechtkommen (bei weiterem nicht alle von Hattie genutzten Meta-Analysen enthalten Angaben zu den Punkten 3 bis 5) und auch hier müssten relativ willkürliche Entscheidungen getroffen werden, z. B. wie hoch der jeweilige Multiplikator angesetzt wird.

Dies zeigt, dass Hatties Studien lediglich grobe Anhaltspunkte bieten - dies ist dem Versuch geschuldet, die Breite der betrachteten Einflussfaktoren zu maximieren.

In den kommenden Newslettern werden wir dieses Thema weiter vertiefen und konkrete Beispiele aus Lernen sichtbar machen bearbeiten.